1
1
2
3
5
8 = (2^2 + 3)
13 = (2^3 + 5) A kettő hatványainak összege 3, vagyis egy Lucas szám.
21 = (2^4 + 5) A kettő hatványainak összege 4, vagyis egy Lucas szám, az 5-ös együtthatók összege 5.
34 = (2^3 + 5) + (2^4 + 5) A kettő hatványainak összege 7, vagyis egy Lucas szám, az 5-ös együtthatók összege 10, (vagyis az előző kettő összege).
55 = (2^3 + 5) + (2^4 + 5) + (2^4 + 5) A kettő hatványainak összege 11, vagyis egy Lucas szám, az 5-ös együtthatók összege 15, (vagyis az előző kettő összege).
89 = (2^3 + 5) + (2^4 + 5) + (2^4 + 5) + (2^3 + 5) + (2^4 + 5) A kettő hatványainak összege 18, vagyis egy Lucas szám, az 5-ös együtthatók összege 25, (vagyis az előző kettő összege).
144 = (2^3 + 5) + (2^4 + 5) + (2^4 + 5) + (2^3 + 5) + (2^4 + 5) + (2^3 + 5) + (2^4 + 5) + (2^4 + 5) A kettő hatványainak összege 29, vagyis egy Lucas szám, az 5-ös együtthatók összege 40, (vagyis az előző kettő összege).
Tehát ha a Fibonacci számokat kettő hatványainak és ötnek az összegeire bontjuk, akkor a kettő hatványkitevőinek az összege mindig egy Lucas számot ad ki, az ötnek az összegei pedig az előző két összegnek az összegei a Fibonacci számok logikájának megfelelően. Ezen felbuzdulva megpróbáltam ugyanígy elemeire bontani a Lucas számokat is, ezúttal a kettő hatványainak és a háromnak az összegeire.
3
4
7 = (2^2 + 3) A kettő hatványainak összege 2, vagyis egy Fibonacci szám.
11 = (2^3 + 3) A kettő hatványainak összege 3, vagyis egy Fibonacci szám.
18 = (2^2 + 3) + (2^3 + 3) A kettő hatványainak összege 5, vagyis egy Fibonacci szám, a hármas együtthatók összege 6, vagyis az előző két szám összege.
29 = (2^2 + 3) + (2^3 + 3) + (2^3 + 3) A kettő hatványainak összege 8, vagyis egy Fibonacci szám, a hármas együtthatók összege 9, vagyis az előző két szám összege.
47 = (2^2 + 3) + (2^3 + 3) + (2^3 + 3) + (2^2 + 3) + (2^3 + 3) A kettő hatványainak összege 13, vagyis egy Fibonacci szám, a hármas együtthatók összege 14, vagyis az előző két szám összege.
Tehát a kettő hatványkitevőinek összegei itt mindig egy Fibonacci számot adnak ki a hármas szám összegei pedig mindig az előző két összeg összegei, mint az imént. Ezután a 3-nál egyel nagyobb 4-es szám összegeit próbáltam hozzáadni a kettő így képzett hatványainak az összegeihez.
8 = (2^2 + 4)
12 = (2^3 + 4)
20 = (2^3 + 4) + (2^2 + 4)
32 = (2^3 + 4) + (2^2 + 4) + (2^3 + 4)
52 = (2^3 + 4) + (2^2 + 4) + (2^3 + 4) + (2^3 + 4) + (2^2 + 4)
Amint láthatjuk kaptunk egy a Fibonacci és a Lucas számokhoz hasonló számsorozatot, ahol szintén mindig a legutolsó két szám összegéből képezzük a következő számot, és ami így egy magasabb rendű Lucas számnak tekinthető mindjárt mondom, hogy miért. Először azonban tegyük meg még egyszer ugyanezt 5 összegeivel is:
9 = (2^2 + 5)
13 = (2^3 + 5)
22 = (2^3 + 5) + (2^2 + 5)
35 = (2^3 + 5) + (2^2 + 5) + (2^3 + 5)
57 = (2^3 + 5) + (2^2 + 5) + (2^3 + 5) + (2^3 + 5) + (2^2 + 5)
Láthatjuk, hogy itt is hasonló eredményre jutottunk, de vajon miért tekinthetőek ezek a számok magasabb rendű Lucas számoknak, és nem csupán önkényesen képzett Fibonacci szerű számsorozatoknak? Ennek a megértéséhez próbáljuk meg kivonni a Fibonacci számokat a Lucas számokból.
3 – 2 = 1
4 – 3 = 1
7 – 5 = 2
11 – 8 = 3
18 – 13 = 5
29 – 21 = 8
47 – 34 = 13
Láthatjuk, hogy Fibonacci számokat kaptunk eredményül, tehát a Lucas számok nem mások, mint két egymásra rétegzett Fibonacci számsor összegei. Most vonjuk ki az általunk képzett magasabb rendű Lucas számokból először a Lucas számokat, majd a második magasabb rendű Lucas számsorból az első magasabb rendű Lucas számsort.
8 – 3 = 5
12 – 4 = 8
20 – 7 = 13
32 – 11 = 21
52 – 18 = 34
9 – 8 = 1
13 – 12 = 1
22 – 20 = 2
35 – 32 = 3
57 – 52 = 5
Láthatjuk, hogy ugyancsak Fibonacci számokat kaptunk eredményül, tehát az így képzett számsorok azért tekinthetőek magasabb rendű Lucas számoknak, mert a Lucas számokhoz hasonlóan szintén egymásra rétegzett Fibonacci számok összegeinek tekinthetőek, és ezt nyilvánvalóan egészen a végtelenségig folytathatjuk, mindig új magasabb rendű Lucas számokat képezve. A magasabb rendű Lucas számok képzésének módszere általam képletbe foglalva, talán nem túl szakszerűen, tehát:
(F2^1 + Fn) = F → ∞ Ahol (F) a Fibonacci számokat jelöli, (n) pedig egy mindig egyel növekvő, változó számot.
Ha pedig a Fibonacci számok felbontásával kapott sorozatok együtthatóihoz adunk hozzá egyet, akkor pedig egészen újfajta sorozatokat kapunk, amelyeket én nem tudok hová tenni.
8 = (2^2 + 4)
14 = (2^3 + 6)
22 = (2^4 + 6)
36 = (2^3 + 6) + (2^4 + 6)
9 = (2^2 + 5)
15 = (2^3 + 7)
24 = (2^4 + 7)
39 = (2^3 + 7) + (2^4 + 7)
Folytassuk tovább a magasabb rendű Lucas számok képzését azáltal, hogy a tényezőire bontott Lucas számok együtthatóihoz mindig hozzáadunk egyet.
2^2 + 6 = 10
2^3 + 6 = 14
…………….. 24
………………38
………………62
………………100
2^2 + 7 = 11
2^3 + 7 = 15
…………….. 41
………………67
………………108
………………175
2^2 + 8 = 12
2^3 + 8 = 16
…………….. 28
………………44
………………72
………………116
………………188
2^2 + 9 = 13
2^3 + 9 = 17
…………….. 30
………………47
………………77
………………124
………………201
2^2 + 10 = 14
2^3 + 10 = 18
…………….. 32
………………50
………………82
………………132
………………346
2^2 + 11 = 15
2^3 + 11 = 19
…………….. 34
………………53
………………87
………………140
………………227
………………367
………………594
2^2 + 12 = 16
2^3 + 12 = 20
…………….. 36
………………56
………………92
………………148
………………240
………………388
………………628
………………1016
2^2 + 13 = 17
2^3 + 13 = 21
…………….. 38
………………59
………………97
………………156
………………253
………………409
………………662
………………1733
2^2 + 14 = 18
2^3 + 14 = 22
…………….. 40
………………62
………………102
………………164
………………266
………………430
………………696
………………1126
………………1822
………………2948
2^2 + 15 = 19
2^3 + 15 = 23
…………….. 42
………………65
………………107
………………172
………………279
………………451
………………730
………………1181
………………1911
………………3092
………………5003
2^2 + 16 = 20
2^3 + 16 = 24
…………….. 44
………………68
………………112
………………180
………………292
………………472
………………764
………………1236
………………2000
………………3236
………………5236
………………8472
Most pedig vegyünk egy átlós metszetet ezeknek a mindig magasabb rendű Lucas számoknak a tagjaiból úgy, hogy először vegyük a legalacsonyabb rendű Lucas számok, vagyis a Fibonacci számok harmadik számát, a kettőt, majd mindig az 1-el magasabb rendű Lucas számok sorban következő számát, amely a hagyományos Lucas számok esetében a három, majd mindig így tegyünk a következő Lucas számok esetében is. Így a következő sorozatot kapjuk:
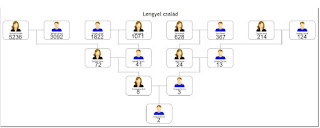
2, 3, 8, 13, 24, 41, 72, 124, 214, 367, 628, 1071, 1822, 3092, 5236
Én ennek a számsornak a nyomán elkészítettem a saját családfámat, ahol, minden családtagot megszámoztam a családfán a fent látható számokkal úgy, hogy én kaptam a kettes számot, tehát az első számot a sorban, majd a családfa hierarchiájában felfelé, az egyes szinteken pedig jobbról bal felé haladva minden családtag meg lett jelölve egy-egy számmal a fenti számsorból a dédszülőkig. Így minden egyes családtagom azonosítható a magasabb rendű Lucas számok eme metszetének egy tagjával, ahogy az alul is látható:
A képre kattintva ki lehet nagyítani a képet. A családfában az egyes tagok matematikai eszközökkel való azonosítására már több módszert is kidolgoztak a tudósok. Ezek közül én most csak egy módszerrel foglalkoznék, még hozzá azzal, amit Németh László nyugalmazott vízügyi mérnök ismertetett Hidrológia és genealógia című előadásában 2016. április 7-én a Bánfalvi fiókkönyvtárban. Én is jelen voltam az előadáson.
Németh módszere arra épül, hogy a családfában elsőként a legfiatalabb családtagot jelöli 1-es számmal. Majd a felsőbb szinteken, így a szülőknél, a nagyszülőknél, illetve a magasabb szinteken a nőből és férfiból álló párokat mindig felváltva 1-essel és 2-essel. Így a négy nagyszülő felváltva 1, 2, 1, 2 számokat kap, a 8 dédszülő pedig felváltva 1, 2, 1, 2, 1, 2, 1, 2 számokat kap. Ez a gyakorlatban valahogy így néz ki:
Ezzel egy jól áttekinthető rendszert kapunk, ahol a számok alapján könnyen megállapíthatjuk, hogy melyik ősünk milyen közel vagy távol, és melyik ágon van tőlünk a családfán. Így például, ha az apai nagyanyai dédapánkat akarjuk azonosítani ezen a családfán, akkor azt könnyen leolvashatjuk a következő számsorból: 212 ahol a kettes az apát, az utána következő egyes az apai nagyanyát, majd az utána következő kettes az apai nagyanyai dédapát jelöli szép sorban.
Kérdés azonban, hogy hogyan azonosíthatunk számokkal egy-egy személyt nemcsak a saját családfánkon belül, hanem az emberiség családfáinak az összességében. Tehát, hogy hogyan azonosíthatjuk be például, hogy nyolcadik ősanyánk ki másnak a nyolcadik ősanyja is egyben, vagy például, hogy a mi kilencedik ősapánknak a lányunokatestvére kinek a kilencedik ősanyja volt.
Ehhez véleményem szerint először is át kell alakítanunk ezt a számozási rendszert. Az egyes szülőházaspárokat itt is ugyanazokkal a számpárokkal jelölöm az egyes szinteken, de a családfa hierarchiájában felfele haladva mindig 1-el növelem a számpáros értékeit. Továbbá az anyai családtagok számértékeit meghagyom plusz értékűeknek, az apai családtagok számértékeit viszont mínuszra változtatom. Így a legfiatalabb családtag most is 1-essel lesz jelölve. A szülők viszont 1-essel és -2-essel. A nagyszülők értékei pedig a következők lesznek: 2, 3, -2, -3 a dédszülők pedig: 3, 4, 3, 4, -3, -4, -3, -4 valahogy így:
Ezt azért kell megtennünk, hogy az emberiség többi tagjának családfái, illetve családfáin szereplő családtagok számértékei összeadhatóak legyenek a mi családfánkon szereplő családtagok számértékeivel, ha az ő családfájuk bármelyik szinten is keresztezi a mi családfánkat, és az így kapott számértékek egyedi értéket kapjanak az összeadás által, mert csak így azonosítható be számszerűen egy közös ős. Nyilvánvalóan a legközelebbi anyai unokatestvérünkkel közösek az anyai nagyszüleink. Viszont ha az én anyai nagyszüleimnek a családfában 1, 2 a számértéke, és a számozási rendszer azonossága miatt az anyai unokatestvérem hasonlóan 2, 1-el jelöli a velem közös nagyszüleit, akkor a számértékeket összeadva 3, 3 értéket kapunk. Ez pedig egy ilyen számozási rendszerben nyilvánvalóan jelzi, hogy itt egy közös ősről van szó. Viszont így már az anyai unokatestvéremmel közös anyai dédszüleim nem lesznek beazonosíthatóak, mert értelemszerűen azoknak a számértékei is 3, 3 értéket fognak kapni és így az értékek nem különülnek el egymástól.
Az apai családtagok mínusz értékbe rakására pedig azért van szükség, mert a rokonsági hálózat minden embernél két felé ágazik, és ha nem különítjük el valahogy az apai családfát az anyai családfától, akkor az anyai családfánk és egy másik családfa metszete, továbbá az apai családfánk és egy másik családfa metszete azonos értéket fognak kapni.
Meg kell oldanunk ezzel kapcsolatban még egy problémát is. Be kell tudnunk azonosítani, hogy milyen távoli rokonunk, tehát negyed, hatok, vagy akár milliomod unokatestvérünk családfájának a mi családfánkkal való metszetét akarjuk megkapni. Ezt pedig csak úgy oldhatjuk meg, hogy mindig, amikor 1-el távolibb unokatestvérünk családfájának a metszetét akarjuk megkapni a mi családfánkkal, akkor 1-el nagyobb számmal kezdjük a családfájának a számozását. Így például az első anyai unokatestvérünk a legközelebbi rokonunk, így számozását a miénknél 1-el nagyobb számmal kezdjük, vagyis kettővel. A szülei számozása 3, 2 lesz, a nagyszüleié pedig 4, 3, 4, 3 lesz a dédszüleié pedig 5, 4, 5, 4, 5, 4, 5, 4 lesz. Valahogy így:
A legközelebbi apai unkatestvérem számozása pedig a fentiekben elmondottak alapján ugyanez lesz csak mínusz értékekben: (-2), (-3, -2), (-4, -3, -4, -3), (-5, -4, -5, -4, -5, -4, -5, -4). Mint arra már fent utaltam ahhoz, hogy egy másik családfa értékei összeadhatóak legyenek a mi családfánk értékeivel, és az eredmény egész érték legyen, azt a másik családfát fordított sorrendben kell számozni a miénkhez képest, ez a képen látszik is. Így az legközelebbi anyai unokatestvéremmel közös nagyszüleink számértékei (4, 3) + (2, 3) = 2.(6, 6) lesznek, a közös nagyapai dédszüleink számértékei pedig (5, 4) + (3, 4) = 2.3:(8, 8) lesz. Ahol a jelzet elején a 2-es és utána a pont azt jelzi, hogy a legközelebbi unokatestvérünkkel közös családfa metszetről van szó. A 3-as és utána a kettőspont pedig azt, hogy a nagyapai dédszülőről van szó és nem a nagyanyairól.
Hogyan azonosíthatjuk egy ilyen számozási rendszerrel egy olyan személyt, aki nem közös ősünk senkivel, de egyik ősünknek, mint például az anyai nagyapánknak az első fiú unokatestvére? Itt két számértéket is rögzítenünk kell, egyrészt azt, hogy az anyai nagyapánknak az első fiú unokatestvére hányadik unokatestvérünknek a nagyapja, illetve rögzítenünk kell az anyai nagyapánknak a számértékeit is a mi családfánkban. Így a számértékek 4.45;1.13 lesz. Tehát a mi negyedik unokatestvérünknek az apai nagyapja, a mi anyai nagyapánknak az első unokatestvére.
Ezzel a módszerrel tehát az emberiség családfáinak egész rendszerében azonosíthatjuk a az egyes személyeket, és ha egyszer talán elkészül az emberiség egész családfája, és ez benne lesz egy nagy számítógépes adatbázisban akkor csak rákeresünk benne a fent leírt jelzetekre, és a számítógép kiadja, hogy a számrendszernek azon a helyén milyen nevű személy van. Visszatérve a magasabb rendű Lucas számokra fent láthattuk, hogy azokkal is beazonosítható a családfánk egy-egy személye és mivel a Lucas számok sorozataiból végtelen sok van az emberiség családfáinak összessége is rögzíthető a magasabb rendű Lucas számok segítségével. Fent vettük a Lucas számok sorozatainak egy átlós metszetét, és azzal számoztuk be a saját családfánkat, így az emberiség többi tagjának családfáját értelemszerűen a rákövetkező metszettel kell megszámozni, mint ahogy az imént mindig 1-el nagyobb számmal kezdtük a mindig távolabbi unokatestvéreink családfájának számozását. Így a magasabb rendű Lucas számok esetében az első unokatestvérünk családfájának számozását a következő számokkal kezdjük, amelyeket a negyedik Fibonacci számból, majd a rákövetkező magasabb rendű Lucas számokból vettünk, és így tovább a végtelenségig. Majd az így kapott számsorozatokat a családfák rendszerében összeadva ugyanígy metszeteket képezhetünk a mi családfánk és más családfák között.
3, 7, 20, 35, 62, 175, 188
A családfák megszámozása magasabb rendű Fibonacci számokkal csak matematikai érdekességnek tekinthető itt. A családfakutatók valószínűleg nem ezt a rendszert fogják használni, ha használni fogják egyáltalán az általam felvázolt rendszert valaha is. Mindenesetre érdemes lenne véleményem szerint matematikai mintákat keresni a magasabb rendű Lucas számokkal megszámozott családfák rendszerében, amit nem én fogok megtenni, hanem a jövő matematikája.
Felhasznált irodalom:
Wikipédia: Fibonacci-számok https://hu.wikipedia.org/wiki/Fibonacci-sz%C3%A1mok
Németh László nyugalmazott vízügyi mérnök Hidrológia és genealógia: vízrendszerek és családfarendszerek összehasonlító vizsgálata című előadása



Nincsenek megjegyzések:
Megjegyzés küldése